Y el desarrollo de trayectoria de un punto de la sección de pala considerada será t' que forma un ángulo α' con el plano de giro de la hélice sin desplazamiento. La tangente α' de α' será análogamente:  tan(α') = a/D'π = e/b' 

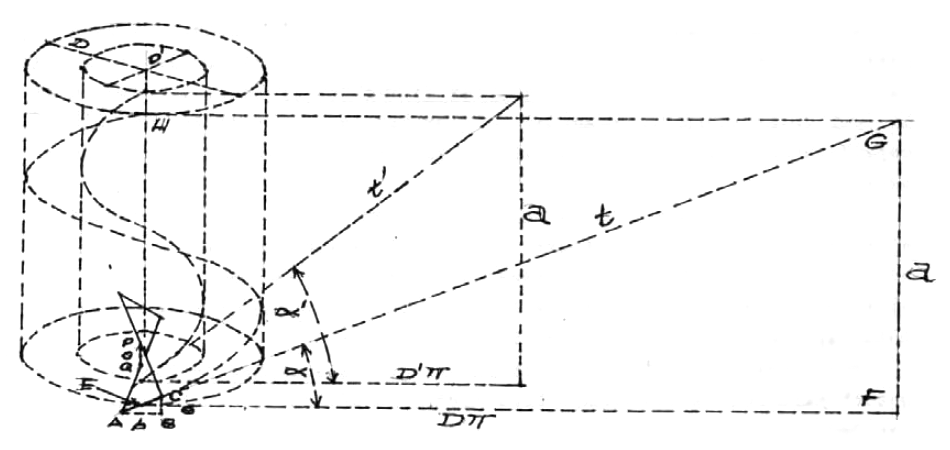
fig. 34

Observamos que el ángulo α va creciendo a medida que nos acercamos al eje de giro. Cuando la sección coincida con el eje de giro, D'=0 ; Y cuando D' tiende a cero, a/D'π tiende a ∞. Y la tangente infinita corresponde a un ángulo de 90°. Este es pues el ángulo que adopta la pala con respecto al plano de giro de la hélice en el centro.

2.7.1.8.5. Molde para construir palas de hélices

Veamos como se puede construir un molde que nos permita moldear rápidamente una pala para hélice de un paso determinado.

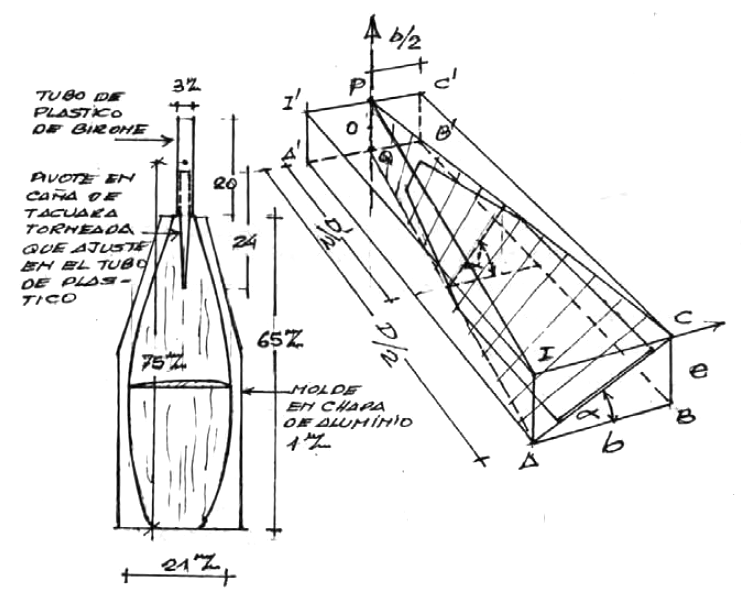
fig. 35

En la figura 35 se reproduce a mayor tamaño la superficie de la pala que contiene los puntos ACPQ de la figura 34. Consideramos el prisma de largo D/2 igual al radio de la hélice y de sección e x b. Estas dimensiones las definimos de la siguiente manera : fijamos el espesor "e" arbitrariamente y calculamos un "b" tal que tan(α)=e/b.

Pero vimos en la expresión (1) que e/b = a/Dπ, en consecuencia

Ulises Alvarez