Si la hélice se atornillara en un sólido su trayectoria seguiría el desarrollo geométrico de la misma, pero al hacerlo en un fluido "patina" avanzando algo menos. El "Paso Absoluto Aerodinámico" es pues menor que el "Paso Absoluto Geométrico". La Fig. 32 muestra el desarrollo de ambas curvas espaciales en el plano.

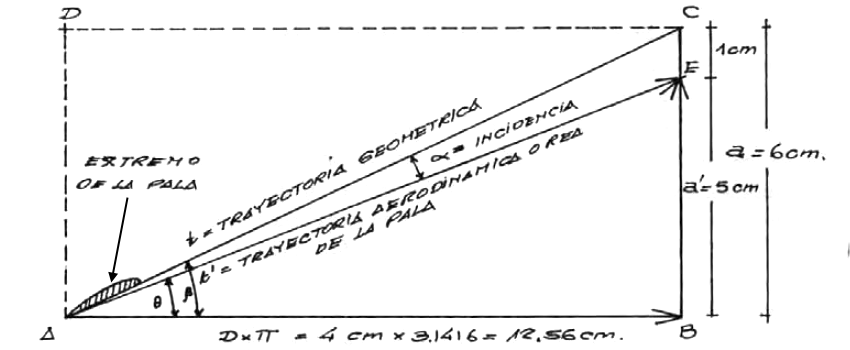
fig. 32

El segmento A-B representa la longitud de la circunferencia que describe la punta de la pala en una rotación igual a D.π (D = diámetro de la hélice); "a" es el avance o paso absoluto geométrico en una rotación completa y C-A = t es la trayectoria geométrica.

De manera similar " a' " es el paso absoluto real o aerodinámico y E-A = t' la trayectoria aerodinámica real del extremo de la pala; β se llama ángulo fijo del extremo de la pala con el plano rotación ; θ es el ángulo que forma la trayectoria real de la punta de la pala con el plano de rotación y α = β - θ el ángulo de incidencia de la pala en su extremo can la corriente de aire relativo.

¿ Qué ángulo de incidencia daremos a las palas ? ... ¿ Adoptaremos un ángulo igual para cada sección de la pala ? ... ¿ Aumentamos la incidencia a medida que nos acercamos al centro o le damos un máximo de incidencia a los 2/3 ? Es aquí donde los especialistas se aferran a sus teorías invocando muy variados razonamientos.

Teóricamente parecería razonable que esta incidencia variara en razón inversa al cuadrado de la velocidad del viento relativo y en razón inversa del área de cada sección elemental de pala a lo largo de la misma a los efectos de obtener un rendimiento equivalente de la hélice en cada elemento de pala, compensando con mayor incidencia la menor velocidad y la menor área de cada uno de estos elementos.

Las hélices así diseñadas tienen óptimo comportamiento pero requieren un cálculo complejo.

Ulises Alvarez