colgado del punto "P". En "b" el mismo péndulo apoyado ahora en el punto "P". En "c" una esfera sobre un plano horizontal. En todos los casos existe un peso "W" actuando en el centro de gravedad, y una reacción "R" aplicada a un punto "P" de soporte del cuerpo. A la derecha de la figura se escriben las condiciones de equilibrio antes mencionadas.

Observamos empero que las tres clases de equilibrio son diferentes.
El de "a" es estable puesto que a poco de separado el péndulo de su posición vertical volverá a ella luego de algunas oscilaciones.
El de "b" es inestable pues a penas separado de la vertical surgirán momentos desequilibrantes que aumentarán la desviación de la vertical.
El de "c" es indiferente pues trasladada la esfera al punto P' del mismo plano horizontal permanecerá en él en equilibrio.

Decimos entonces que un cuerpo y en especial un avión o aeromodelo es estable, cuando apartado de la situación de equilibrio en que se encuentra volando, surgen fuerzas y momentos equilibrantes que tienden a restituir esa situación de equilibrio.

Es inestable cuando apartado de esa condición de equilibrio sumen fuerzas y momentos que tienden a desequilibrarlo más.

Y es indiferente cuando apartado de la situación de equilibrio permanece en ella.

3.2.1. Equilibrio y estabilidad longitudinal

En la figura 87 se muestran las fuerzas que actúan sobro un avión o aeromodelo en vuelo : W = peso del aparato aplicado en el centro de gravedad ; L = fuerza de sustentación con un brazo de palanca "a" respecto de C.G. ; T = fuerza de tracción de la hélice con brazo de palanca "b" respecto de C.G. ; D = resultante de las fuerzas que "resisten" el movimiento con brazo de palanca "c" respecto de C.G. ; F = fuerza sustentadora o desustentadora del estabilizador con brazo de palanca "d" respecto de C. G.

Llamemos positivas las fuerzas dirigidas hacia arriba, negativas las dirigidas hacia abajo. Llamemos momento positivo aquel que origina un tiro de cabreo y negativo el que produce uno de picado.

Para que el vuelo resulte horizontal deberán cumplirse las condiciones de equilibrio de fuerzas y momentos. Y adoptando momentos respecto de C. G. tendremos :

+ L - W ∓ E = 0
+ T - D = 0
- L.a + T.b + D.c ∓ E.d = 0

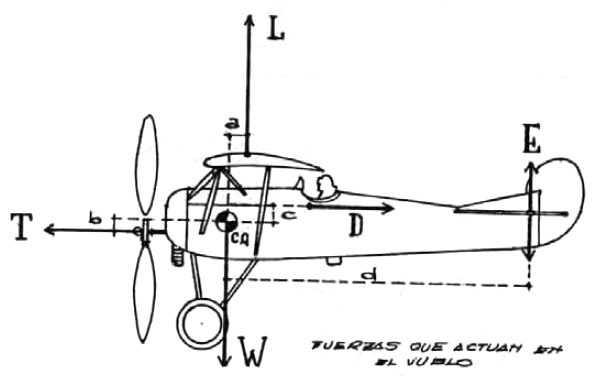
fig. 87 - El Arte Del Peanut Scale

Ulises Alvarez